- (1) Un sistema está en equilibrio mecánico cuando la suma de fuerzas y momentos, sobre cada partícula del sistema es cero.
- (2) Un sistema está en equilibrio mecánico si su posición en el espacio de configuración es un punto en el que el gradiente de energía potencial es cero.
- EQUILIBRIO DE FUERZAS
- Como consecuencia de las leyes de la estática una partícula en
equilibrio no sufre aceleración lineal ni de rotación, pero puede estar moviéndose a velocidad uniforme o
rotar a veocidad angular uniforme. Esto es
ampliable a un sólido rígidoLas ecuaciones
necesarias y suficientes de equilibrio mecánico son:
- Una partícula o un sólido rígido está en equilibrio cuando: la suma de todas las fuerzas que actúan sobre el cuerpo es cero.

- En el espacio se tienen tres ecuaciones de fuerzas, una por dimensión; descomponiendo cada fuerza en sus coordenadas resulta:
- Y como un vector, es cero, cuando cada una de sus componentes es cero, se tiene:
- Un sólido rígido está en equilibrio de traslación cuando la suma de las componentes de las fuerzas que actúan sobre él es cero.
- Un sólido rígido está en equilibrio, si la suma de momentos sobre el cuerpo es cero.
- En el espacio tiene las tres ecuaciones una por dimensión; por un
razonamiento similar al de las fuerzas:
- Resultando:
- Un sólido rígido está en equilibrio de rotación cuando la suma de las componentes de los momentos que actúan sobre él es cero
Se distingue un tipo particular de equilibrio mecánico llamado equilibrio estático que correspondería a una situación en que el cuerpo está en reposo, con velocidad cero: una hoja de papel sobre un escritorio estará en equilibrio mecánico y estático, un paracaidista cayendo a velocidad constante, dada por la velocidad estaría en equilibrio mecánico pero no estático.
ESTABILIDAD DEL EQUILIBRIO
El análisis de la estabilidad del equilibrio puede llevarse a cabo estudiando los mínimos y máximos locales (extremos locales) de la función de energía potencial
- Un punto es de equilibrio inestable, si la segunda derivada de la energía potencial < 0 y por tanto la energía potencial tiene un máximo local. Si el sistema sufre un desplazamiento de su posición de equilibrio, por pequeño que éste sea, entonces se alejará más y más de él (de ahí el nombre inestabilidad para esa situación).
- Un punto es de equilibrio indiferente o neutral, si la segunda derivada = 0, entonces se encuentra una región donde la energía no varía. Así, si el sistema es desplazado de la posición de equilibrio una cantidad suficientemente pequeña, posiblemente no volverá a acercarse al equilibrio pero tampoco divergerá mucho de la posición anterior de equilibrio.
- Un punto es de equilibrio estable si la segunda derivada > 0 y por tanto la energía potencial tiene un mínimo local. La respuesta del sistema frente a pequeñas perturbaciones o un alejamiento arbitrariamente pequeño de del punto de equilibrio es volver u oscilar alrededor del punto de equilibrio. Si existe más de un punto de equilibrio estable para un sistema, entonces se dice que cualquiera de ellos cuya energía potencia es mayor que el mínimo absoluto representa un estado metaestable
- Equilibrio estable, se da cuando la forma cuadrática Q(x1,...,xn) es definida positiva y, por tanto, todos sus autovalores son números positivos.
- Equilibrio totalmente inestable, se da cuando la forma cuadrática Q(x1,...,xn) es definida negativa, por tanto, todos sus autovalores son negativos.
- Equilibrio mixto inestable, se da cuando la forma cuadrática Q(x1,...,xn) es no es definida positiva y alguno de sus autovalores es negativo. Esto implica que según ciertas direcciones puede haber estabilidad unidimensional pero según otras habrá inestabilidad unidimensional
MÉTODO EXPERIMENTAL DEL EQUILIBRIO ESTÁTICO
En el siguiente experimento se presenta una situación que parece desafiar la gravedad. Consiste en un soporte de acrílico con un agujero que permite sostener una botella de vino de forma casi horizontal.
Materiales & Equipos
- Botella de vino
- Soporte de acrílico
Descripción del experimento
El montaje del experimento se presenta en la siguiente figura, en donde se observa que a pesar de que el soporte de acrílico se encuentra inclinado respecto a la vertical, la botella queda suspendida de manera horizontal. El sistema se encuentra en equilibrio estático.
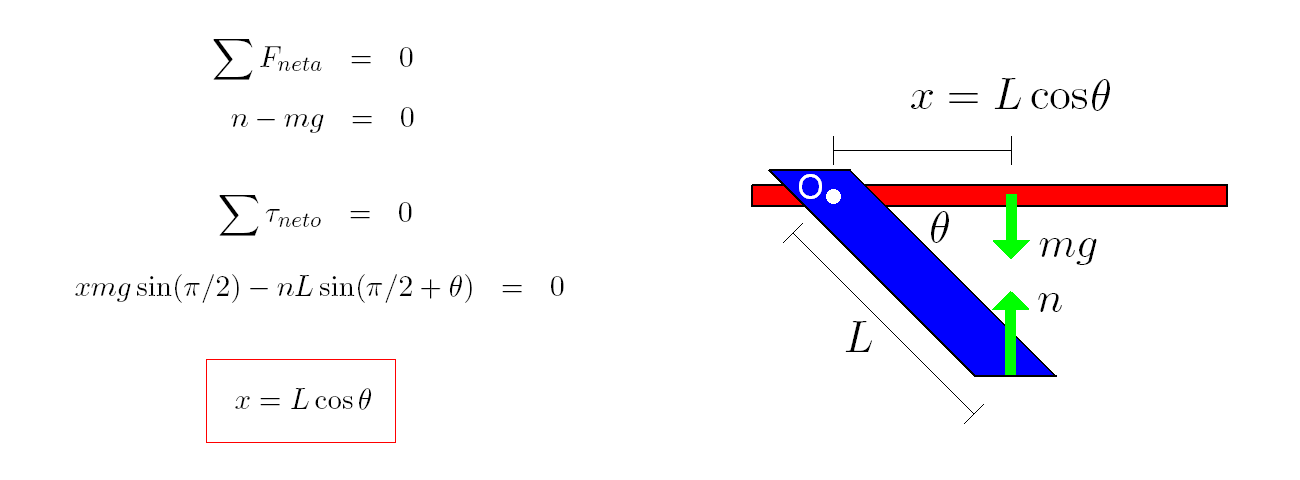







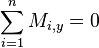


No hay comentarios:
Publicar un comentario